Follow @solverworld Tweet this
You may have seen the following equation:
\begin{align}
\lim_{n \rightarrow \infty} \left( 1 +\frac{1}{n} \right)^n = \mathrm{e}.
\end{align}
which expresses the fundamental constant e as a limit. Wondering how that can be proven?
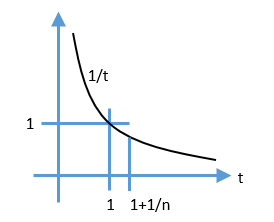
Consider this graph:
\begin{align}
\int_1^{x} \, \frac{1}{t} \mathrm{d}t = \ln x
\end{align}
Looking at the graph, you can see that the area under the \(\frac{1}{t}\) curve on the interval \((1,1+\frac{1}{n})\) is bounded by
\begin{align}
\frac{1}{n}\left( \frac{1}{1+\frac{1}{n}} \right) \leq \int_1^{1+\frac{1}{n}} \, \frac{1}{t} \mathrm{d}t \leq \frac{1}{n} \left( 1 \right)
\end{align}
Using the definition of \(\ln x\) above, we have
\begin{align}
\frac{1}{1+n} \leq \ln \left( 1+\frac{1}{n} \right) \leq \frac{1}{n}
\end{align}
Raising \(\mathrm{e}\) to the power of each term,
\begin{align}
\mathrm{e}^{(\frac{1}{1+n})} \leq 1+\frac{1}{n} \leq \mathrm{e}^{(\frac{1}{n})}
\end{align}
Raising each term to power \(n\),
\begin{align}
\mathrm{e}^{(\frac{n}{1+n})} \leq \left( 1+\frac{1}{n} \right)^n \leq \mathrm{e}
\end{align}
As n approaches infinity, the left hand term approaches \(\mathrm{e}\), therefore
\begin{align}
\lim_{n \rightarrow \infty} \left( 1 +\frac{1}{n} \right)^n = \mathrm{e}.
\end{align}
QED.